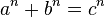En teoría de números, el último teorema de Fermat, o teorema de Fermat-Wiles, es uno de los teoremas más famosos en la historia de la matemática. Utilizando la notación moderna, se puede enunciar de la siguiente manera:
Si n es un número entero mayor que 2, entonces no existen números enteros a, b y c, tales que se cumpla la igualdad (con a,b,c no nulos): 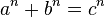
Teorema de Fermat: (en general) Para: xn ± yn = zn
x, y, z pertenecen a los naturales (incluyendo el cero), n pertenece a los naturales (sin incluir el cero)
Entonces: “No existen soluciones enteras para n > 2.”
simplificándolo adoptamos solo la forma general (que es más usada): xn + yn = zn
x, y, z pertenecen a los naturales (incluyendo el cero), n pertenece a los naturales sin incluir el cero) y para esta: “No existen soluciones enteras para n > 2.”
Ejemplos:
El enunciado del último Teorema de Fermat (1601-1665) quedó anotado en un margen de su ejemplar de la Aritmética de Diofanto de Alejandría (150 A.C.) traducida al latín por Claude Gaspar Bachet (1581-1638) publicado en 1621. Este libro, con las numerosas notas marginales de Fermat, fue publicado en 1670 por su hijo Clemente Samuel. El enunciado del teorema dice que la ecuación
no tiene soluciones enteras para n>2. Fermat afirma que tenía una demostración, pero se exime de darla argumentado que el márgen es demasiado estrecho como para dárnosla.
Recientemente, en 1995, Wiles demostró este teorema. Para entender mejor este teorema veamos el caso n=2, para el cual existen soluciones enteras.
Hagamos cuatro filas de números (esquema 1). En la primera van los números naturales 1,2,…; en la segunda sus cuadrados 1, 4, 9, …; en la tercera la diferencia entre los cuadrados vecinos 3, 5, 7, …; en la cuarta las diferencias de las diferencias 2, 2, …